[ad_1]
An vital and controversial subject within the space of private pockets safety is the idea of “brainwallets” – storing funds utilizing a non-public key generated from a password memorized solely in a single’s head. Theoretically, brainwallets have the potential to supply nearly utopian assure of safety for long-term financial savings: for so long as they’re saved unused, they don’t seem to be weak to bodily theft or hacks of any variety, and there’s no strategy to even show that you simply nonetheless keep in mind the pockets; they’re as secure as your very personal human thoughts. On the identical time, nevertheless, many have argued in opposition to the usage of brainwallets, claiming that the human thoughts is fragile and never properly designed for producing, or remembering, lengthy and fragile cryptographic secrets and techniques, and so they’re too harmful to work in actuality. Which aspect is correct? Is our reminiscence sufficiently strong to guard our personal keys, is it too weak, or is probably a 3rd and extra fascinating chance really the case: that all of it is dependent upon how the brainwallets are produced?
Entropy
If the problem at hand is to create a brainwallet that’s concurrently memorable and safe, then there are two variables that we have to fear about: how a lot info we have now to recollect, and the way lengthy the password takes for an attacker to crack. Because it seems, the problem in the issue lies in the truth that the 2 variables are very extremely correlated; in actual fact, absent a couple of sure particular sorts of particular methods and assuming an attacker operating an optimum algorithm, they’re exactly equal (or reasonably, one is exactly exponential within the different). Nevertheless, to begin off we will deal with the 2 sides of the issue individually.
A typical measure that laptop scientists, cryptogaphers and mathematicians use to measure “how a lot info” a chunk of information accommodates is “entropy”. Loosely outlined, entropy is outlined because the logarithm of the variety of potential messages which might be of the identical “type” as a given message. For instance, take into account the quantity 57035. 57035 appears to be within the class of five-digit numbers, of which there are 100000. Therefore, the quantity accommodates about 16.6 bits of entropy, as 216.6 ~= 100000. The quantity 61724671282457125412459172541251277 is 35 digits lengthy, and log(1035) ~= 116.3, so it has 116.3 bits of entropy. A random string of ones and zeroes n bits lengthy will comprise precisely n bits of entropy. Thus, longer strings have extra entropy, and strings which have extra symbols to select from have extra entropy.
Alternatively, the quantity 11111111111111111111111111234567890 has a lot lower than 116.3 bits of entropy; though it has 35 digits, the quantity isn’t of the class of 35-digit numbers, it’s within the class of 35-digit numbers with a really excessive degree of construction; an entire checklist of numbers with at the very least that degree of construction could be at most a couple of billion entries lengthy, giving it maybe solely 30 bits of entropy.
Data idea has quite a lot of extra formal definitions that attempt to grasp this intuitive idea. A very widespread one is the concept of Kolmogorov complexity; the Kolmogorov complexity of a string is mainly the size of the shortest laptop program that may print that worth. In Python, the above string can be expressible as ‘1’*26+’234567890′ – an 18-character string, whereas 61724671282457125412459172541251277 takes 37 characters (the precise digits plus quotes). This provides us a extra formal understanding of the concept of “class of strings with excessive construction” – these strings are merely the set of strings that take a small quantity of information to specific. Observe that there are different compression methods we will use; for instance, unbalanced strings like 1112111111112211111111111111111112111 might be minimize by at the very least half by creating particular symbols that characterize a number of 1s in sequence. Huffman coding is an instance of an information-theoretically optimum algorithm for creating such transformations.
Lastly, notice that entropy is context-dependent. The string “the fast brown fox jumped over the lazy canine” could have over 100 bytes of entropy as a easy Huffman-coded sequence of characters, however as a result of we all know English, and since so many hundreds of data idea articles and papers have already used that actual phrase, the precise entropy is probably round 25 bytes – I’d seek advice from it as “fox canine phrase” and using Google you’ll be able to determine what it’s.
So what’s the level of entropy? Primarily, entropy is how a lot info you must memorize. The extra entropy it has, the tougher to memorize it’s. Thus, at first look it appears that you really want passwords which might be as low-entropy as potential, whereas on the identical time being onerous to crack. Nevertheless, as we’ll see beneath this mind-set is reasonably harmful.
Power
Now, allow us to get to the following level, password safety in opposition to attackers. The safety of a password is greatest measured by the anticipated variety of computational steps that it might take for an attacker to guess your password. For randomly generated passwords, the best algorithm to make use of is brute drive: strive all potential one-character passwords, then all two-character passwords, and so forth. Given an alphabet of n characters and a password of size ok, such an algorithm would crack the password in roughly nok time. Therefore, the extra characters you utilize, the higher, and the longer your password is, the higher.
There may be one strategy that tries to elegantly mix these two methods with out being too onerous to memorize: Steve Gibson’s haystack passwords. As Steve Gibson explains:
Which of the next two passwords is stronger, safer, and tougher to crack?
You most likely know this can be a trick query, however the reply is: Even though the primary password is HUGELY simpler to make use of and extra memorable, it is usually the stronger of the 2! Actually, since it’s one character longer and accommodates uppercase, lowercase, a quantity and particular characters, that first password would take an attacker roughly 95 instances longer to search out by looking out than the second impossible-to-remember-or-type password!
Steve then goes on to write down: “Just about everybody has at all times believed or been advised that passwords derived their power from having “excessive entropy”. However as we see now, when the one out there assault is guessing, that long-standing frequent knowledge . . . is . . . not . . . appropriate!” Nevertheless, as seductive as such a loophole is, sadly on this regard he’s useless fallacious. The reason being that it depends on particular properties of assaults which might be generally in use, and if it turns into extensively used assaults might simply emerge which might be specialised in opposition to it. Actually, there’s a generalized assault that, given sufficient leaked password samples, can robotically replace itself to deal with nearly something: Markov chain samplers.
The best way the algorithm works is as follows. Suppose that the alphabet that you’ve consists solely of the characters 0 and 1, and you realize from sampling {that a} 0 is adopted by a 1 65% of the time and a 0 35% of the time, and a 1 is adopted by a 0 20% of the time and a 1 80% of the time. To randomly pattern the set, we create a finite state machine containing these possibilities, and easily run it again and again in a loop.
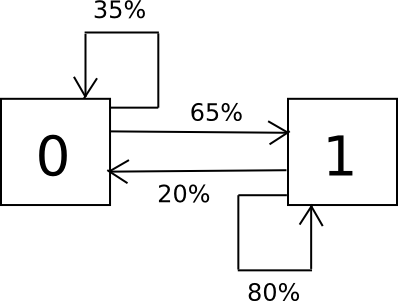
Here is the Python code:
import random i = 0 whereas 1: if i == 0: i = 0 if random.randrange(100) < 35 else 1 elif i == 1: i = 0 if random.randrange(100) < 20 else 1 print i
We take the output, break it up into items, and there we have now a method of producing passwords which have the identical sample as passwords that folks really use. We are able to generalize this previous two characters to an entire alphabet, and we will even have the state preserve observe not simply of the final character however the final two, or three or extra. So if everybody begins making passwords like “D0g…………………”, then after seeing a couple of thousand examples the Markov chain will “study” that folks usually make lengthy strings of durations, and if it spits out a interval it’s going to usually get itself quickly caught in a loop of printing out extra durations for a couple of steps – probabilistically replicating folks’s conduct.
The one half that was unnoticed is how you can terminate the loop; as given, the code merely offers an infinite string of zeroes and ones. We might introduce a pseudo-symbol into our alphabet to characterize the tip of a string, and incorporate the noticed price of occurrences of that image into our Markov chain possibilities, however that is not optimum for this use case – as a result of way more passwords are quick than lengthy, it might often output passwords which might be very quick, and so it might repeat the quick passwords hundreds of thousands of instances earlier than making an attempt a lot of the lengthy ones. Thus we’d need to artificially minimize it off at some size, and improve that size over time, though extra superior methods additionally exist like operating a simultaneous Markov chain backwards. This basic class of methodology is often known as a “language model” – a likelihood distribution over sequences of characters or phrases which might be as easy and tough or as complicated and complex as wanted, and which may then be sampled.
The basic purpose why the Gibson technique fails, and why no different technique of that sort can probably work, is that within the definitions of entropy and power there may be an fascinating equivalence: entropy is the logarithm of the variety of prospects, however power is the variety of prospects – briefly, memorizability and attackability are invariably precisely the identical! This is applicable no matter whether or not you might be randomly deciding on characters from an alphabet, phrases from a dictionary, characters from a biased alphabet (eg. “1” 80% of the time and “0” 20% of the time, or strings that observe a specific sample). Thus, plainly the search for a safe and memorizable password is hopeless…
Easing Reminiscence, Hardening Assaults
… or not. Though the essential concept that entropy that must be memorized and the area that an attacker must burn via are precisely the identical is mathematically and computationally appropriate, the issue lives in the actual world, and in the actual world there are a selection of complexities that we will exploit to shift the equation to our benefit.
The primary vital level is that human reminiscence isn’t a computer-like retailer of information; the extent to which you’ll precisely keep in mind info usually is dependent upon the way you memorize it, and in what format you retailer it. For instance, we implicitly memorize kilobytes of data pretty simply within the type of human faces, however even one thing as comparable within the grand scheme of issues as canine faces are a lot tougher for us. Data within the type of textual content is even tougher – though if we memorize the textual content visually and orally on the identical time it is considerably simpler once more.
Some have tried to benefit from this reality by producing random brainwallets and encoding them in a sequence of phrases; for instance, one may see one thing like:
witch collapse observe feed disgrace open despair creek highway once more ice least
A popular XKCD comic illustrates the precept, suggesting that customers create passwords by producing 4 random phrases as an alternative of making an attempt to be intelligent with image manipulation. The strategy appears elegant, and maybe taking away of our differing means to recollect random symbols and language on this method, it simply may work. Besides, there’s an issue: it would not.
To cite a recent study by Richard Shay and others from Carnegie Mellon:
In a 1,476-participant on-line research, we explored the usability of 3- and 4-word system- assigned passphrases compared to system-assigned passwords composed of 5 to six random characters, and 8-character system-assigned pronounceable passwords. Opposite to expectations, sys- tem-assigned passphrases carried out equally to system-assigned passwords of comparable entropy throughout the usability metrics we ex- amined. Passphrases and passwords had been forgotten at comparable charges, led to comparable ranges of person problem and annoyance, and had been each written down by a majority of contributors. Nevertheless, passphrases took considerably longer for contributors to enter, and seem to require error-correction to counteract entry errors. Passphrase usability didn’t appear to extend after we shrunk the dictionary from which phrases had been chosen, diminished the variety of phrases in a passphrase, or allowed customers to vary the order of phrases.
Nevertheless, the paper does depart off on a notice of hope. It does notice that there are methods to make passwords which might be increased entropy, and thus increased safety, whereas nonetheless being simply as simple to memorize; randomly generated however pronounceable strings like “zelactudet” (presumably created through some type of per-character language mannequin sampling) appear to supply a average acquire over each phrase lists and randomly generated character strings. A probable reason for that is that pronounceable passwords are prone to be memorized each as a sound and as a sequence of letters, rising redundancy. Thus, we have now at the very least one technique for bettering memorizability with out sacrificing power.
The opposite technique is to assault the issue from the alternative finish: make it tougher to crack the password with out rising entropy. We can’t make the password tougher to crack by including extra mixtures, as that will improve entropy, however what we will do is use what is called a tough key derivation function. For instance, suppose that if our memorized brainwallet is b, as an alternative of creating the personal key sha256(b) or sha3(b), we make it F(b, 1000) the place F is outlined as follows:
def F(b, rounds): x = b i = 0 whereas i < rounds: x = sha3(x + b) i += 1 return x
Primarily, we preserve feeding b into the hash operate again and again, and solely after 1000 rounds can we take the output.

Feeding the unique enter again into every spherical isn’t strictly needed, however cryptographers advocate it so as to restrict the impact of assaults involving precomputed rainbow tables. Now, checking every particular person password takes a thousand time longer. You, because the legit person, will not discover the distinction – it is 20 milliseconds as an alternative of 20 microseconds – however in opposition to attackers you get ten bits of entropy without cost, with out having to memorize something extra. In the event you go as much as 30000 rounds you get fifteen bits of entropy, however then calculating the password takes near a second; 20 bits takes 20 seconds, and past about 23 it turns into too lengthy to be sensible.
Now, there may be one intelligent method we will go even additional: outsourceable ultra-expensive KDFs. The thought is to provide you with a operate which is extraordinarily costly to compute (eg. 240 computational steps), however which might be computed not directly with out giving the entity computing the operate entry to the output. The cleanest, however most cryptographically sophisticated, method of doing that is to have a operate which may in some way be “blinded” so unblind(F(blind(x))) = F(x) and blinding and unblinding requires a one-time randomly generated secret. You then calculate blind(password), and ship the work off to a 3rd get together, ideally with an ASIC, after which unblind the response once you obtain it.
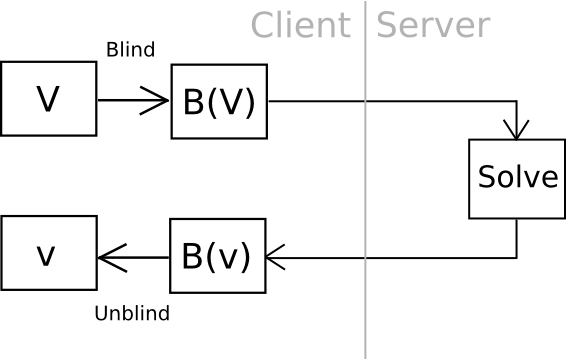
One instance of that is utilizing elliptic curve cryptography: generate a weak curve the place the values are solely 80 bits lengthy as an alternative of 256, and make the onerous drawback a discrete logarithm computation. That’s, we calculate a worth x by taking the hash of a worth, discover the related y on the curve, then we “blind” the (x,y) level by including one other randomly generated level, N (whose related personal key we all know to be n), after which ship the end result off to a server to crack. As soon as the server comes up with the personal key akin to N + (x,y), we subtract n, and we get the personal key akin to (x,y) – our supposed end result. The server doesn’t study any details about what this worth, and even (x,y), is – theoretically it may very well be something with the proper blinding issue N. Additionally, notice that the person can immediately confirm the work – merely convert the personal key you get again into some extent, and ensure that the purpose is definitely (x,y).
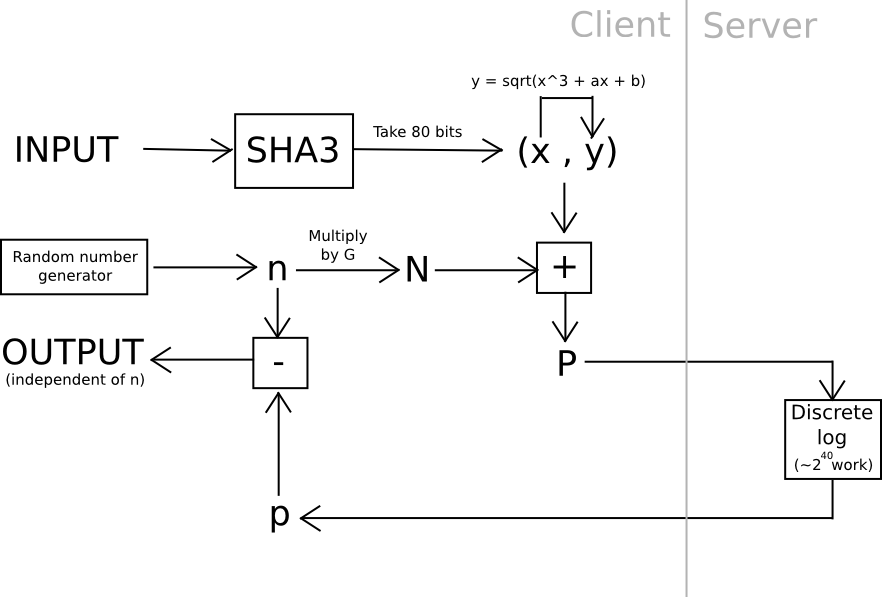
One other strategy depends considerably much less on algebraic options of nonstandard and intentionally weak elliptic curves: use hashes to derive 20 seeds from a password, apply a really onerous proof of labor drawback to every one (eg. calculate f(h) = n the place n is such that sha3(n+h) < 2^216), and mix the values utilizing a reasonably onerous KDF on the finish. Except all 20 servers collude (which might be prevented if the person connects via Tor, since it might be inconceivable even for an attacker controlling or seeing the outcomes of 100% of the community to find out which requests are coming from the identical person), the protocol is safe.
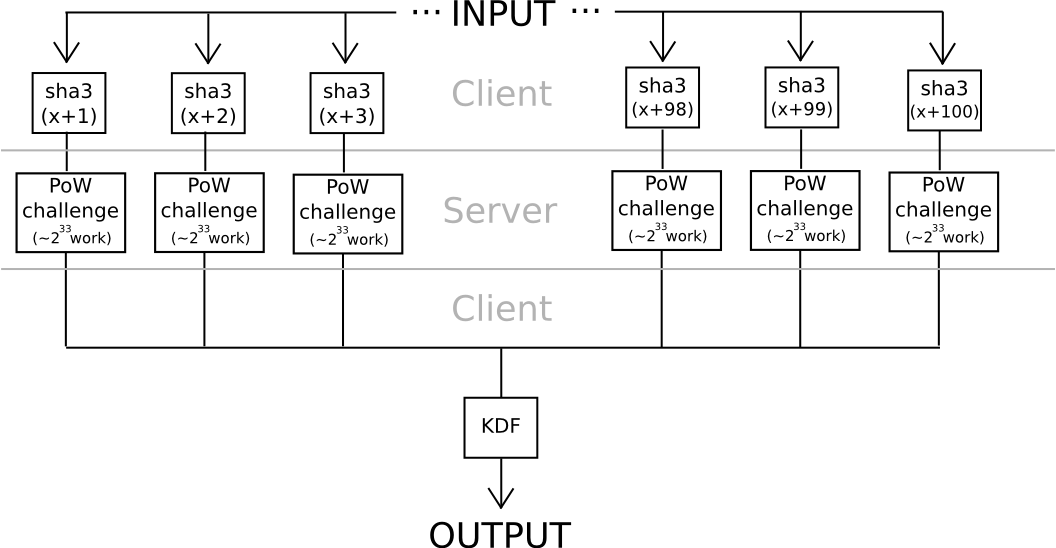
The fascinating factor about each of those protocols is that they’re pretty simple to show right into a “helpful proof of labor” consensus algorithm for a blockchain; anybody might submit work for the chain to course of, the chain would carry out the computations, and each elliptic curve discrete logs and hash-based proofs of labor are very simple to confirm. The elegant a part of the scheme is that it turns to social use each customers’ bills in computing the work operate, but additionally attackers’ a lot better bills. If the blockchain sponsored the proof of labor, then it might be optimum for attackers to additionally attempt to crack customers’ passwords by submitting work to the blockchain, by which case the attackers would contribute to the consensus safety within the course of. However then, in actuality at this degree of safety, the place 240 work is required to compute a single password, brainwallets and different passwords could be so safe that nobody would even hassle attacking them.
Entropy Differentials
Now, we get to our ultimate, and most fascinating, memorization technique. From what we mentioned above, we all know that entropy, the quantity of data in a message, and the complexity of assault are precisely similar – except you make the method intentionally slower with costly KDFs. Nevertheless, there may be one other level about entropy that was talked about in passing, and which is definitely essential: skilled entropy is context-dependent. The identify “Mahmoud Ahmadjinejad” may need maybe ten to fifteen bits of entropy to us, however to somebody residing in Iran whereas he was president it may need solely 4 bits – within the checklist of crucial folks of their lives, he’s fairly probably within the high sixteen. Your mother and father or partner are utterly unknown to myself, and so for me their names have maybe twenty bits of entropy, however to you they’ve solely two or three bits.
Why does this occur? Formally, one of the simplest ways to consider it’s that for every particular person the prior experiences of their lives create a type of compression algorithm, and underneath totally different compression algorithms, or totally different programming languages, the identical string can have a special Kolmogorov complexity. In Python, ‘111111111111111111’ is simply ‘1’*18, however in Javascript it is Array(19).be a part of(“1”). In a hypothetical model of Python with the variable x preset to ‘111111111111111111’, it is simply x. The final instance, though seemingly contrived, is definitely the one which greatest describes a lot of the actual world; the human thoughts is a machine with many variables preset by our previous experiences.
This reasonably easy perception results in a very elegant technique for password memorizability: attempt to create a password the place the “entropy differential”, the distinction between the entropy to you and the entropy to different folks, is as giant as potential. One easy technique is to prepend your personal username to the password. If my password had been to be “yui&(4_”, I’d do “vbuterin:yui&(4_” as an alternative. My username may need about ten to fifteen bits of entropy to the remainder of the world, however to me it is nearly a single bit. That is primarily the first purpose why usernames exist as an account safety mechanism alongside passwords even in instances the place the idea of customers having “names” isn’t strictly needed.
Now, we will go a bit additional. One frequent piece of recommendation that’s now generally and universally derided as nugatory is to choose a password by taking a phrase out of a e book or track. The explanation why this concept is seductive is as a result of it appears to cleverly exploit differentials: the phrase may need over 100 bits of entropy, however you solely want to recollect the e book and the web page and line quantity. The issue is, in fact, that everybody else has entry to the books as properly, they usually can merely do a brute drive assault over all books, songs and flicks utilizing that info.
Nevertheless, the recommendation isn’t nugatory; in actual fact, if used as solely half of your password, a quote from a e book, track or film is a superb ingredient. Why? Easy: it creates a differential. Your favourite line out of your favourite track solely has a couple of bits of entropy to you, however it’s not everybody’s favourite track, so to your entire world it may need ten or twenty bits of entropy. The optimum technique is thus to choose a e book or track that you simply actually like, however which can be maximally obscure – push your entropy down, and others’ entropy increased. After which, in fact, prepend your username and append some random characters (even perhaps a random pronounceable “phrase” like “zelactudet”), and use a safe KDF.
Conclusion
How a lot entropy do you must be safe? Proper now, password cracking chips can carry out about 236 attempts per second, and Bitcoin miners can carry out roughly 240 hashes per second (that is 1 terahash). The complete Bitcoin community collectively does 250 petahashes, or about 257 hashes per second. Cryptographers typically take into account 280 to be a suitable minimal degree of safety. To get 80 bits of entropy, you want both about 17 random letters of the alphabet, or 12 random letters, numbers and symbols. Nevertheless, we will shave fairly a bit off the requirement: fifteen bits for a username, fifteen bits for a very good KDF, maybe ten bits for an abbreviation from a passage from a semi-obscure track or e book that you simply like, after which 40 extra bits of plan outdated easy randomness. In the event you’re not utilizing a very good KDF, then be happy to make use of different substances.
It has change into reasonably widespread amongst safety consultants to dismiss passwords as being basically insecure, and argue for password schemes to get replaced outright. A typical argument is that due to Moore’s regulation attackers’ energy will increase by one little bit of entropy each two years, so you’ll have to carry on memorizing increasingly more to stay safe. Nevertheless, this isn’t fairly appropriate. In the event you use a tough KDF, Moore’s regulation lets you take away bits from the attacker’s energy simply as shortly because the attacker good points energy, and the truth that schemes resembling these described above, apart from KDFs (the average variety, not the outsourceable variety), haven’t even been tried suggests that there’s nonetheless some strategy to go. On the entire, passwords thus stay as safe as they’ve ever been, and stay very helpful as one ingredient of a powerful safety coverage – simply not the one ingredient. Reasonable approaches that use a mix of {hardware} wallets, trusted third events and brainwallets could even be what wins out in the long run.
[ad_2]
Source link
